Minimizing the length of a loop, part 2: Energies and Forces
In the first part of this tutorial, we used Morpho to create an irregular loop. In this section, we’re going to tell Morpho that we want to minimize its length while keeping the area it encloses constant.
Quantities such as the length of a loop, the area enclosed etc., are examples of mathematical objects called functionals, i.e. they can all be expressed as integrals of some function over the loop. Morpho has many of these built in, and new functionals can be easily defined. Here are a few of them:—
linetension — the length of the loop.
enclosedarea — the area enclosed by a loop.
surfacetension — the area of a surface.
enclosedvolume — the volume enclosed by a surface.
To tell Morpho that we want to minimize the length of the loop, type
[code gutter=”false” lang=”js”]lt=new(linetension)
m.addenergy(lt)[/code]
The first line creates a new linetension object and assigns it to a variable lt. The second tells the loop you created in the last tutorial to treat this functional as an energy to be minimized.
The area constraint is made in a similar fashion,
[code gutter=”false” lang=”js”]la=new(enclosedarea)
m.addconstraint(la)[/code]
where we use a different variable, la, to refer to the enclosedarea object. Note that we use a different selector, addconstraint to tell the loop that this functional is a constraint to be maintained.
Before we perform the minimization, we can check which functionals are currently active by typing
[code gutter=”false” lang=”js”]m.showfunctionals()[/code]
which returns
energy <linetension>
constraint <enclosedarea>
<body>
We can also find out their current numerical value by typing,
[code gutter=”false” lang=”js”]m.evaluatefunctional(lt)[/code]
which returns the current numerical length of the loop:
10.5174
Exercise 1. Determine the area enclosed by the loop using m.evaluatefunctional.
You can also find the total energy by typing
[code gutter=”false” lang=”js”]m.totalenergy()[/code]
which will again give the total length of the loop as it stands. In general, a shape in Morpho can have many functionals, not just one, and totalenergy will automatically add them all up.
From the given energy, Morpho can automatically compute the force on each point in the loop. To perform the minimization, Morpho will slide each point a small amount in the direction of this force, recompute the forces, and repeat this sequence until the loop reaches a stable shape.
It’s helpful to understand what direction these forces actually point in a given configuration, and Morpho provides a helpful way of visualizing them:
[code gutter=”false” lang=”js”]show(m.visualizeforces(lt, scale=0.5))[/code]
which will display something like
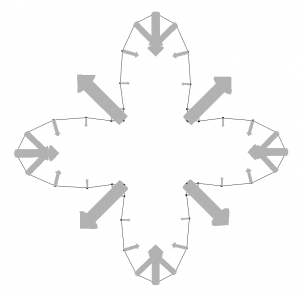 showing the points at the “tips” are being pulled inwards, while those closest to the center are being pushed outwards. We can change the arguments to visualizeforces to change the length of the arrows, and also which functional is being visualized.
showing the points at the “tips” are being pulled inwards, while those closest to the center are being pushed outwards. We can change the arguments to visualizeforces to change the length of the arrows, and also which functional is being visualized.
Exercise 2. Visualize the forces exerted by the area constraint.
To begin minimizing the length of the loop, type
[code gutter=”false” lang=”js”]m.linesearch()[/code]
which moves all points in the loop in the direction of the force caused by the linetension while maintaining the enclosedarea constraint.
Exercise 3. Verify that this has reduced the total energy.
You can see the effect on the loop with
[code gutter=”false” lang=”js”]show(m)[/code]
but the effect from only one step is pretty subtle. To take a bunch of steps, we enclose the call to linesearch in a loop:
[code gutter=”false” lang=”js”]do(m.linesearch();, {i,20})[/code]
Here, we take 20 further steps after which the loop looks like
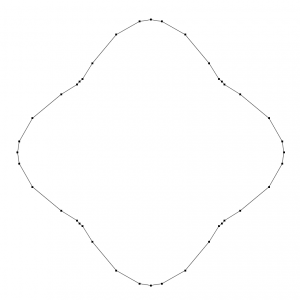 which is definitely approaching a circle!
which is definitely approaching a circle!
Exercise 4. Look again at the forces due to the two functionals in this new configuration.
To get to the solution, simply continue taking further steps. Something like
[code gutter=”false” lang=”js”]do(m.linesearch();, {i,100})[/code]
is enough to get to the solution:—
Exercise 5. What’s the energy now? Verify that taking further steps doesn’t appreciably change the solution we’ve found.
The minimization worked, but you might notice that the points in the loop are very irregularly spaced. This is aesthetically unpleasant, but it also has an important consequence: Morpho’s numerical representation of the solution, which should be a perfect circle, is quite poor. For more complex problems, this can sometimes cause Morpho to get stuck and fail to find the true solution; even in this simple problem it has meant we have had to take many more steps than absolutely necessary.
In the next section of the tutorial, we’ll introduce how Morpho helps us handle this problem, and investigate the consequences more carefully.
