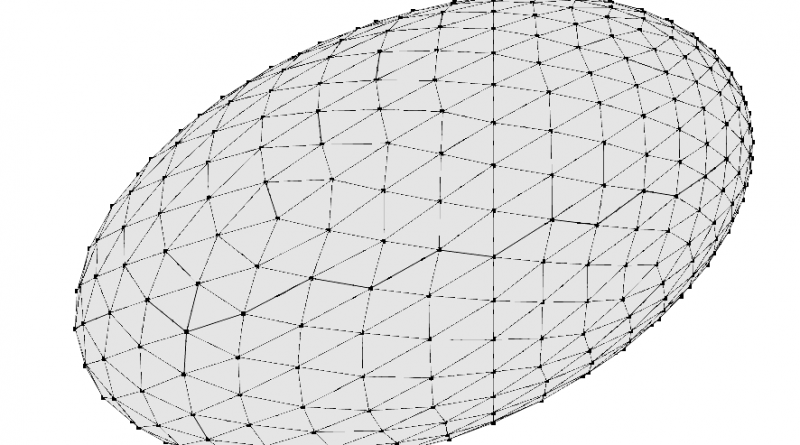
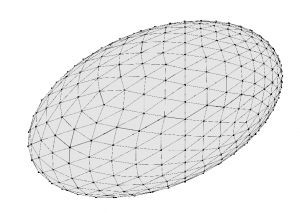
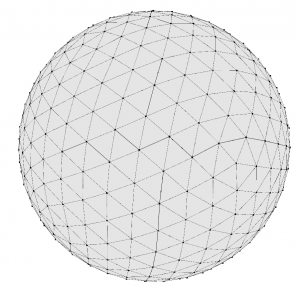
Minimizing an ellipsoidal bubble

The three-dimensional equivalent of the loop example is to minimize the area of a closed surface at constant volume. Just as the two-dimensional problem led to a circular loop, the answer is a sphere. There’s many ways to solve this problem with Morpho, however, and here we’ll import a predefined mesh.

Download the ellipsoid.mesh example mesh, move to the directory that contains it, start up Morpho and type

[code lang=”js” gutter=”false”]m=manifoldload("ellipsoid.mesh")[/code]

to load the mesh. Use show() to display it and you’ll see that this file contains an ellipsoid

To perform the minimization, we need to take the following steps:—

1. Create functionals for surface area and enclosed volume (they’re called surface tension and enclosed volume respectively in morpho)
2. Tell morpho that we want to use one of these as an energy to be minimized, and the other as a constraint.
3. Eventually we will want to include regularization functionals as well.
4. Perform the minimization.
5. Visualize the results.

Exercise 1. Using the script you made in the loop minimization example as a starting point, try to modify this script to minimize the ellipsoid. Ignore regularization for now.

Hints: You’ll need quite a few minimization steps using linesearch()-I used 1000. If you include show() in your script, you can watch the minimization happen interactively!

My solution is posted below (click to expand).

[code lang=”js” gutter=”false” collapse=”true” title=”Minimize an area at constant volume”]
Nsteps=1000 // Number of steps to take

// Create the manifold
m=manifoldload("ellipsoid.mesh")
show(m)

// Add surface tension
la=new(surfacetension)
m.addenergy(la)

// Keep the volume enclosed constant
lv=new(enclosedvolume)
m.addconstraint(lv)

initial=m.totalenergy()

// Perform the minimization
do(
m.linesearch();
, {i,Nsteps})

final=m.totalenergy()

print("Energy change ", final-initial)
[/code]

and the result looks like this:

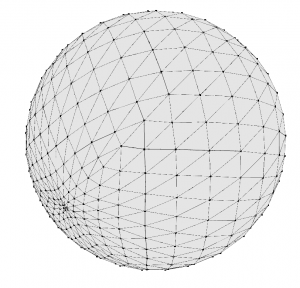
Just as with the loop example, notice that the mesh points have become very bunched in the portion of the sphere that was originally the ends of the initial ellipsoid. The fix is very similar.

Exercise 2. Regularize your minimization using the functional equiarea to promote equal sized elements. You’ll need to create an object, tell Morpho to use it as a regularization and include it in your minimization loop. Look again at how we regularized the two dimensional loop example to get the necessary syntax if you don’t remember it. Note that you will need fewer steps for this one!

Here’s the solution:

[code lang=”js” gutter=”false” collapse=”true” title=”Minimize an area at constant volume with regularization”]
Nsteps=200 // Number of steps to take

// Create the manifold
m=manifoldload("ellipsoid.mesh")
show(m)

// Add surface tension
la=new(surfacetension)
m.addenergy(la)

// Keep the volume enclosed constant
lv=new(enclosedvolume)
m.addconstraint(lv)

//Promote equal sized segments
le=new(equiarea);
m.addregularization(le);

initial=m.totalenergy()

// Perform the minimization
do(
m.linesearch();
m.linesearch(le);
, {i,Nsteps})

final=m.totalenergy()

print("Energy change ", final-initial)
[/code]

and the resulting shape

no longer exhibits the “bunching” phenomenon.