Directed by Fulton Gonzalez
Spectral Graph Theory is the study of the properties of a graph through the properties of the eigenvalues and eigenvectors of matrices associated with the graph, most importantly the graph Laplacian and its variants. Numerous papers have appeared in the recent literature on
this subject, especially since it has powerful and wide-ranging applications, such as in data mining, clustering, and segmentation, shape matching and recognition, and even differential geometry.
There are many theorems in the spectral theory of partial differential operators that turn out to have counterparts in spectral graph theory, and this project will focus on the exploration of one possible extension: the relation of graph Laplacians with mean value operators and group theory.
Let ![]() be a simple graph, which can have either finite or infinitely many vertices. (By simple, we mean that the edges of
be a simple graph, which can have either finite or infinitely many vertices. (By simple, we mean that the edges of ![]() are undirected, there is no more than one edge between two vertices, and no edge starts and ends at the same point.) Consider the following sample graph:
are undirected, there is no more than one edge between two vertices, and no edge starts and ends at the same point.) Consider the following sample graph:

Let us order its vertices and edges. This order can be arbitrary, and the purpose is to assign rows and columns to the matrices we’ll define. For example, in the sample graph above, our vertices are ordered ![]() , and our edges are ordered
, and our edges are ordered ![]() . Next, to our graph we associate three matrices: the adjacency matrix
. Next, to our graph we associate three matrices: the adjacency matrix ![]() , the degree matrix
, the degree matrix ![]() , and the incidence matrix
, and the incidence matrix ![]() .
.
The adjacency matrix of ![]() is a symmetric square matrix whose rows and columns correspond to the vertices of our graph, and where the
is a symmetric square matrix whose rows and columns correspond to the vertices of our graph, and where the ![]() entry is
entry is ![]() if vertex
if vertex ![]() and vertex
and vertex ![]() are joined by an edge, and is
are joined by an edge, and is ![]() otherwise. Here is the adjacency matrix of our sample graph:
otherwise. Here is the adjacency matrix of our sample graph:

The degree matrix ![]() is a diagonal matrix whose rows and columns correspond to the vertices of our graph, and whose
is a diagonal matrix whose rows and columns correspond to the vertices of our graph, and whose ![]() -entry is the degree of the vertex
-entry is the degree of the vertex ![]() : this is the number of edges emanating from the vertex
: this is the number of edges emanating from the vertex ![]() . For our sample graph, the degree matrix is
. For our sample graph, the degree matrix is
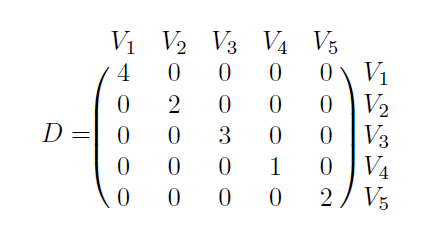
Finally, the incidence matrix ![]() of
of ![]() is a matrix whose rows correspond to the edges of
is a matrix whose rows correspond to the edges of ![]() and whose columns correspond to the vertices of
and whose columns correspond to the vertices of ![]() . The entries of
. The entries of ![]() are given as follows. Suppose that edge
are given as follows. Suppose that edge ![]() has endpoints
has endpoints ![]() and
and ![]() , with
, with ![]() . Then
. Then
![Rendered by QuickLaTeX.com \[ s_{il}=\begin{cases} +1&\text{ if }l=j\ -1&\text{ if }l=k\ 0&\text{ if }l\neq j\text{ or }k \end{cases}\]](https://sites.tufts.edu/verseimreu/wp-content/ql-cache/quicklatex.com-f7a50ed2dc4394b903b9403cf9337147_l3.png)
Thus for our sample graph above, the incidence matrix is
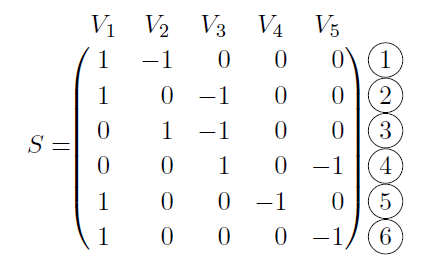
If ![]() is the number of vertices of
is the number of vertices of ![]() , then the graph Laplacian of
, then the graph Laplacian of ![]() is the
is the ![]() matrix
matrix
![]()
It is easy to show that
The graph Laplacian ![]() is singular and has nonnegative eigenvalues. Thus
is singular and has nonnegative eigenvalues. Thus ![]() is always an eigenvalue, and the column matrix
is always an eigenvalue, and the column matrix
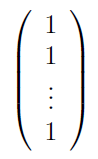
If a graph ![]() has vertex set
has vertex set ![]() , then a function on
, then a function on ![]() can be identified with an
can be identified with an ![]() column vector
column vector
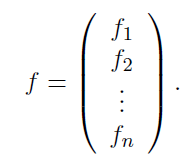
Here ![]() . A function
. A function ![]() on
on ![]() is called harmonic if
is called harmonic if ![]() .
.
There has been a lot of recent interest in graph Laplacians, and their associated eigenvalues and eigenvectors, due to their relation with the large scale geometries of graphs as well as their applications to, for example, data science. They are the natural discrete analogues of the Laplace operator in ![]() :
:
![]()
Graph Laplacians share several of the properties of the Euclidean Laplacian. The goal of this project is to study some further analogues to Euclidean Laplacians, such as mean value properties, which are obvious at distance
desired background
The prerequisite for successful participation in this project is a solid background in multivariable calculus and linear algebra, as well as some familiarity with theorem-proving.