Graph Modeling Algorithms: A Spectral Approach

by Liam Thomas

Mentor: Abiy Tasissa, Mathematics; funding source: Provost’s Office

thomasliamc_38699_2264900_Final-Poster.pptx

Graph theory studies the mathematical properties of graphs, which are essentially sets of dots, called nodes, that are connected by lines, called edges. Graph theory in its modern form was first developed in the 18th century by Leonhard Euler, who was attempting to solve what was known as the “Bridges of Königsberg” problem. This was a famous open problem at the time, which asked whether it was possible to traverse all seven bridges of the Prussian city of Königsberg in a single walk without crossing any single bridge twice. See the image below:

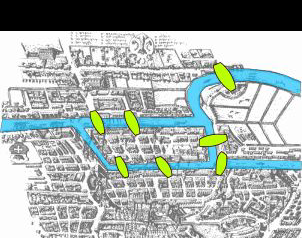
Euler proved that this was indeed not possible, and in the process inadvertently “invented” (or discovered) graph theory, by considering the bridges of the city as a system of nodes and edges. Our research this summer was devoted to the graph matching problem , which concerns finding similarities between two different graphs as quickly as possible. This is accomplished via algorithms, which themselves have to take into account essential properties of the two graphs with efficiency and precision. Thus, it is helpful to use patterns and facts from the discipline of
pure graph theory when designing such algorithms.

Our approach to this problem relies heavily on the sub-discipline of spectral graph theory . Each graph can be described with matrices (i.e. square tables of numbers), and associated with these matrices is a spectrum of numbers. We use theorems from the field of linear algebra, which studies matrices, to glean insights about the properties of the associated graphs and thereby construct a distance known as the diffusion distance . In addition to some theorems from spectral graph theory, we use random walks , which measure the path of a random series of hops around the nodes of the graph, to generate this distance.

Once we’ve measured our diffusion distance of the two graphs, we compare the diffusion distances of the two graphs so that we can measure how different their structures are. Then we measure their structure another way: by seeing which nodes are connected to which other nodes, putting this information into an object called an adjacency matrix , and seeing how similar the two adjacency matrices are.

At this point, we have two measures of difference for the two graphs: the diffusion distance and the adjacency matrix. We can then apply conventional algorithms from the field of convex optimization to solve the graph matching problem in optimal time. Finally, two objects make up the output of this algorithm: first, a matrix which tells us how to shuffle the second graph to return it to the form of the first graph, and second, another matrix which tells us exactly how “different” the two graphs are using the measurements described.