Fractals
Orthogonal Polynomials on Fractals
Directed by Gamal Mograby and Kasso Okoudjou
Project Description
[latexpage]
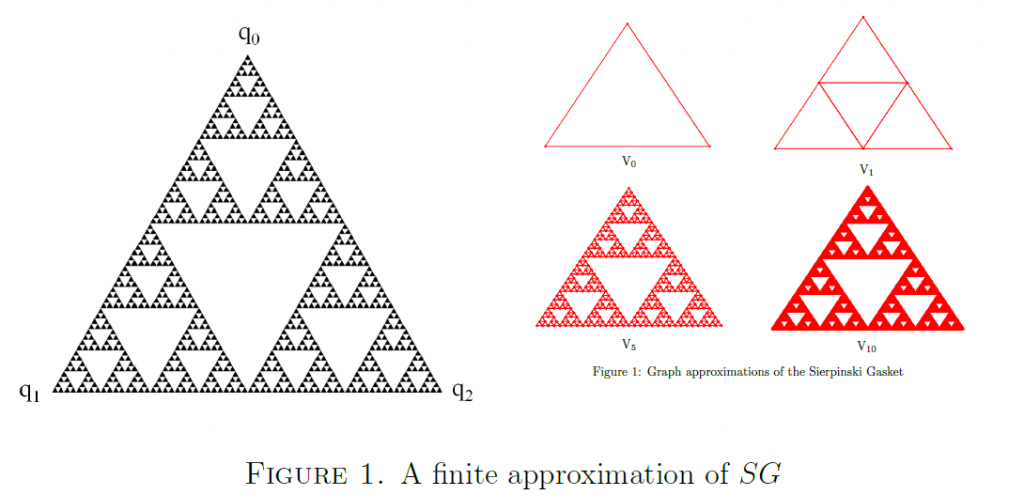
In this project, students will learn the theory of calculus on a rather interesting set: a fractal set. In particular, we will focus on the Sierpinski Gasket ($SG$)
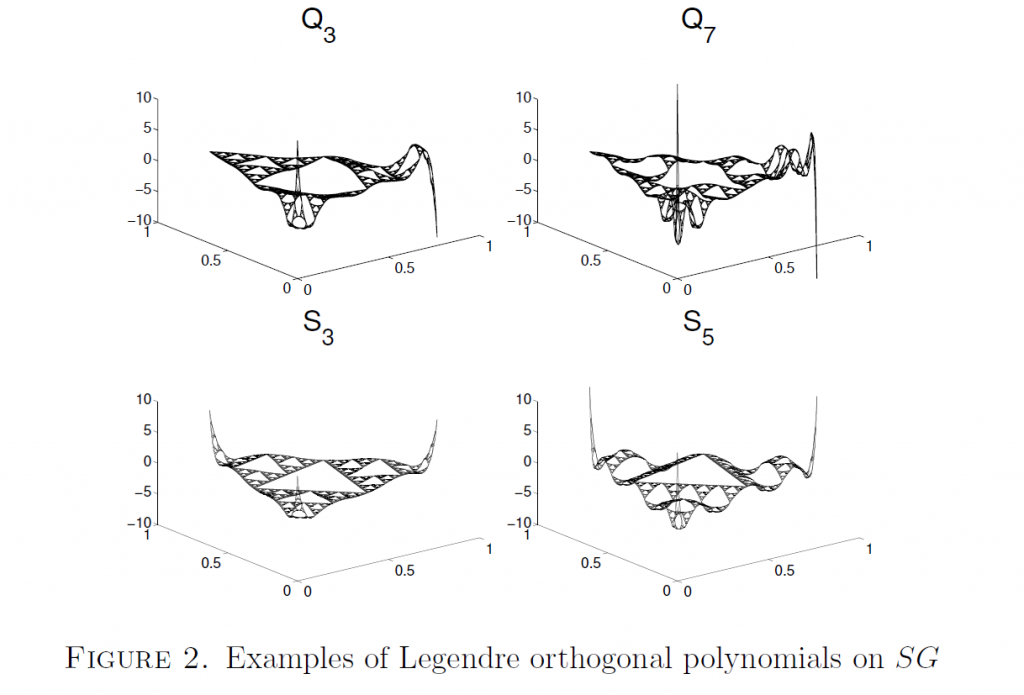
We will learn how to develop some calculus notions on $SG$. The starting point is the construction of an operator, $\Delta$, called the Laplacian operator, and which is analogous to the second derivative operator we learned in calculus. Subsequently, we will learn how to solve differential equations such as $-\Delta u(x)=\lambda u(x)$, leading to a theory of Fourier series on $SG$. We can then l define the space of polynomial of degree less than or equal to $j$ as the set of solutions of the equation $\Delta^{j+1} u(x)=0$. Our goal this summer will be to construct sequences of orthogonal polynomials with respect to various inner products. In the past students have worked on constructing such orthogonal polynomials on $SG$ (see Figure 2) that are analog of the classical Legendre orthogonal polynomials on $[-1, 1]$.
Desired Background
This summer we will continue investigating orthogonal polynomials on $SG$. In particular, we will focus on constructing the analogs of the Chebyshev orthogonal polynomials. We will build on preliminary work by former students. To be successful in this research project, students must have had a course in linear algebra, differential equations, and the calculus sequence. In addition, familiarity with some programming language would be helpful, but not required. But more importantly, students curious and eager to learn something new are highly encouraged to apply for this project.