Frame Theory

Finite Frames and Frame Potentials

Directed by Kasso Okoudjou

In this project, students will work to design and analyze systems for effective and efficient signal and data representations. The problems students will investigate are related to frame theory. A finite frame of a d−dimensional vector space ℍ is a spanning set, which allows the analysis and synthesis of vectors in a way similar to basis decompositions. However, frames are redundant systems and as such the reconstruction formulas they provide are not unique. This redundancy plays a key role in many applications of frames which appear now in a range of areas that include, but is not limited to, signal processing, quantum computing, coding theory, and sparse representations, see [2, 4, 5, 6] for an overview.

One set of problems concerns the extremal sets of vectors for the family of p^th potential functionals defined as follows. Given N unit-norm vectors {f_k}_k=1^N in a d−dimensional vector space ℍ, and given p ∈ (0,∞], the p^th frame potential is

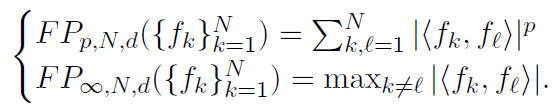
When p = 2, FP_2,N,d is called the frame potential and its minimizers are called finite unit norm tight frames (FUNTFs) [1]. Examples of FUNTs include the platonic solids.

The characterization of the minimizers of the p^th frame potentials in the case ℍ = ℝ² is still incomplete ([3]), and will be one of the problems students will investigate. More generally, the students will be asked to characterize the minimizers of FP_p,N,d when d ≥ 3. In particular, they will search for universal minimizers, that is, sets that are optimal for a large range of p when N and d are fixed? Students will attempt to construct and/or characterize the minimizers of the p^th frame potentials for specific values of p, e.g., the case p = ∞ is very interesting and subject to a number of fascinating open questions. Students will explore these questions both theoretically and numerically. Students interested in this project are expected to have some familiarity with linear algebra, multivariable calculus, and some computer programing, e.g., Matlab.

This project will be directed by Dr. Kasso Okoudjou, who is passionate about introducing undergraduate students to research in the mathematical sciences. He is excited by the opportunity to share his love of mathematics with you this summer.

References