Geometric Group Theory (GGT)
Computational Aspects of Geometric Group Theory
Directed by Kim Ruane and Genevieve Walsh
Recommended Book to get yourself ready: “Groups, Graphs and Trees”
by John Meier. The link is https://www.cambridge.org/core/books/groups-graphs-and-trees/4D0D919000500E7ED9964962EEFCB871
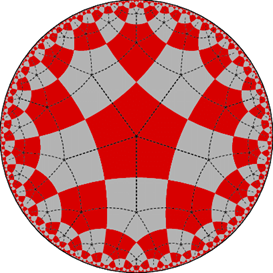
Description: We’ll use computational group theory and hyperbolic geometry tools (GAP, MAGMA, and SnapPY) to understand interesting subgroups of infinite groups. We are focusing on certain well-known classes of groups, right-angled Coxeter and right-angled Artin groups. The figure above is a fundamental domain for a right-angled Coxeter group. We’ll start off by studying group presentations, Cayley graphs, and geometric examples. We’ll finish up by analyzing some specific kernels of maps to Z, and natural extensions of this.
Topics may include:
- What algorithms are and how they can be used effectively in group theory;
- Learn how to use the computer program GAP and understand how the algorithms for this program work;
- Investigate how subgroups and various types of growth of subgroups can be detected;
- Normal forms and effective algorithms.
The students will become familiar with GAP and also with lim, a program that maps the orbits under Fuchsian and Kleinian groups.
Level of Students and prerequisites: A beginning course in abstract algebra, including basic group theory. Exceptions may be considered.
Who we are: Kim Ruane and Genevieve Walsh: We are experienced researchers in geometric group theory and topology who have “supervised” many students at various stages. We love to see what students bring to the table.