Directed by Christoph Börgers

Project Description

We will use differential equations and computers to examine questions in biology.

Examples of possible projects (we’ll do what sounds most interesting to you!): 

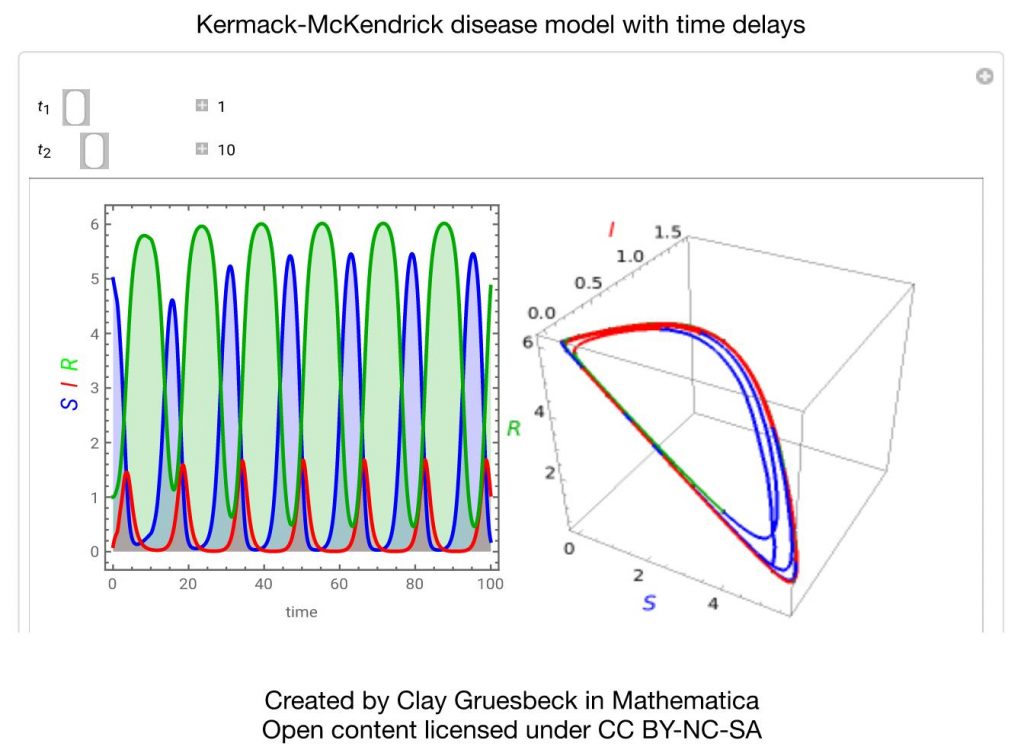
  1. The simplest model of epidemics is called the Kermack-McKendrick model (Figure 1). It is a system of differential equations. It does not have solutions in which the infection rate stays nearly constant for a long time. However, early in the Covid pandemic, infection rates (at least in some states in the U.S.) remained fairly constant for a surprisingly long time. Can this be reconciled with the Kermack-McKendrick model by modifying the model to reflect the assumption that people and public health officials become more cautious as infections rise, less cautious as they fall? 
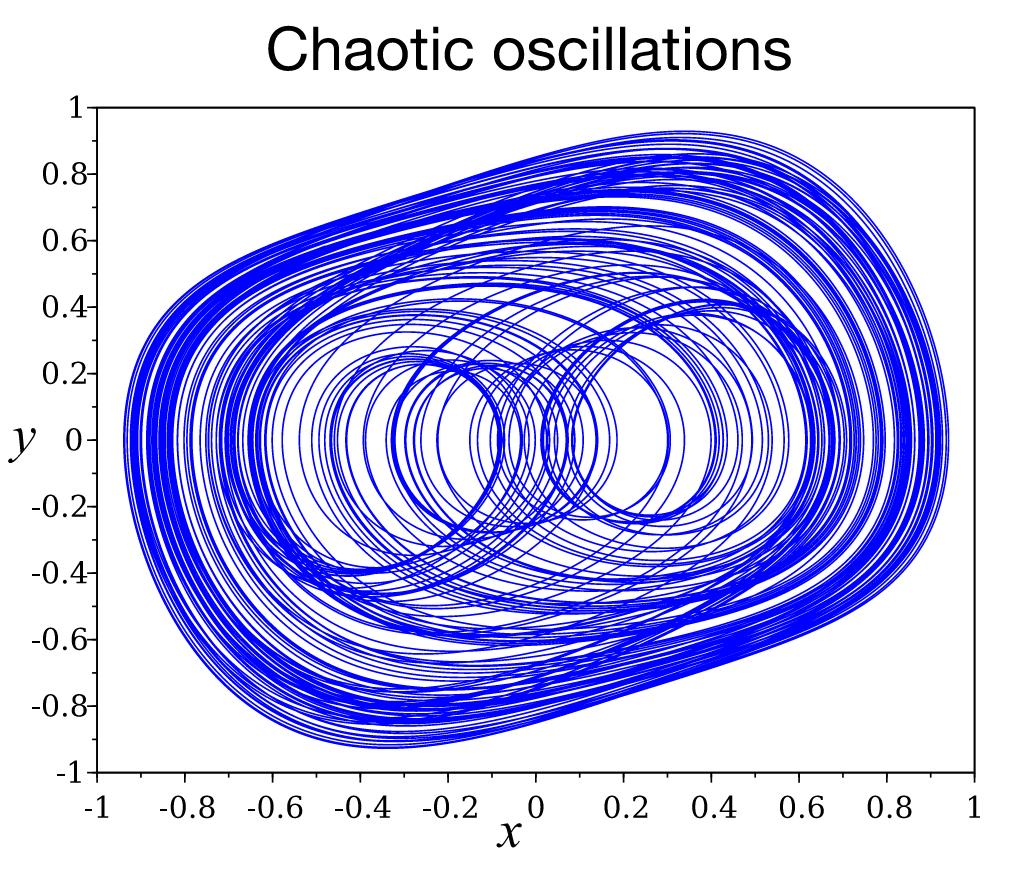
Figure 1. Visualization of the Kermack-McKendrick Disease Model
  1. Solutions of systems of many differential equations very often exhibit chaotic behavior. (They change erratically, seemingly randomly and unpredictably, even though nothing in the equations is random.) Neuronal networks in the brain are modeled using hundreds, thousands, or millions of differential equations, yet hardly anybody in computational neuroscience talks about chaos. Why is that? Starting with an extensive library of Matlab code that I have created, we’ll look for traces of chaos in simulations of neuronal networks, and think about whether chaos might be useful or detrimental to the effective function of brain networks. 
Figure 2. A graph of oscilations from a chaotic dynamical system
  1. After observing an animal population for 50 years, can we deduce (approximately) how likely the population is to go extinct in the next 20 years? This question has many different facets. Its study will involve probability theory, since animal populations are subject to seemingly random fluctuations. A big part of the question is: Can we make useful deductions about the nature of the random fluctuations by observing a relatively short (50-year) time series? And what if the nature of the random fluctuations itself varies with time, for instance because “outlying” events become more common — as they do, in the real world, because of climate change? You would ideally have a little bit of background in probability already, but if not, I’ll teach you. 
Figure 3. A cute endangered animal, though not one that we’ll be discussing.

The goals are:

  • You get introduced to modeling using calculus and differential equations.
  • You learn about differential equations, numerical analysis, coding, probability. 
  • With luck, you discover something new and exciting. 
  • Most importantly, however, you have a wonderful summer!
Desired Background

The prerequisites are calculus, and some experience programming in Matlab, Python, C, C++, or a similar language. If you have learned about differential equations, that will be helpful. If not, I’ll teach you.